What makes quantum computing that different

The Why, the How, and the What

As Richard Feynman said, no one really understands quantum mechanics. I have done a lot of research work for writing this article, and I hope it could give you a head start to explore the amazing quantum world. But if you find it hard to understand, well, that is normal. I also found quantum theory weird and hard to believe.

What makes quantum computers different from classical computers?

You may have heard that quantum computers are fast. Yes, they are fast. Months ago, Google’s quantum computer has proven that it can solve certain types of problems 1.5 billion times faster than the top supercomputer on Earth. But the interesting thing about quantum computers is that they are not just fast. They behave the same way as described in quantum theory that you will see below and that makes it fundamentally different than a classical computer. A quantum computer can do something that is impossible for any classical computers. Those quantum properties make it very useful for some use cases.

What can quantum computers do?

Because of their quantum properties, quantum computers are really good at certain tasks. For other tasks, we will leave it to classical computers. So what are the tasks that quantum computers good at? Here are some example use cases that people are already using quantum computers for.

Design safer airplanes

The first use case is to design airplanes. The design of airplanes is very complicated. It involves simulation of many possible environment conditions. It’s like playing chess, which also involves a lot of possible outcomes. There are simple too many possibilities to simulate on a classical computer, so people are already trying to design airplane on quantum computers.

More accurate weather forecast

Another complex problem is weather forecasting, which has even more possibilities to simulate than airplane design. This is because of the so-called “butterfly effect”, or more formally, the chaos theory. In weather forecasting, if there is a slight error in measurement, for example, if we miss to record a butterfly moving its wings in a city, the forecast result could be completely wrong. So, to make an accurate weather forecast, we need to simulate a huge number of possibilities, which could only be done on a quantum computer.

Develop better medicines

The third example is similar to the previous two. To design medicines, we need to consider the effect of a lot of possible chemical combinations, which can only be done using simulations. Again, that is an easy task for quantum computers.

Break encryption

One more example is to break encryption. All kinds of encryption rely on the fact that factorization is hard. Factorization means to find the prime factors of a given number. For example, the prime factors of 15 is 3 and 5. What makes factorization hard is that there is no known ways to factor any number. The only way is to use brute-force, which is extremely slow on a classical computer. Quantum computers are proved to be exponentially faster than classical computers.

So now you may start worrying about how to keep your secrets safe. Don’t worry, people already developed quantum encryption and it is proved that there is no way to break it. We will see why in below sections.

Why would we care? Why now?

In year 1962, John Kennedy gave a now famous speech, also known as the Moon speech.

7 years later, we were on the Moon. It took only 7 years to make impossible tasks become possible. Very soon, we could use quantum computers to make the world a better place to live. We could have safer airplanes and better medicines, thanks to quantum computers.

Real quantum computers

Let me give you some examples of real quantum computers. The image above shows model 2000Q from D-Wave, a Japanese company. This quantum computer is located at Tokyo. It has 2,000 qubits in it. Qubit means quantum bit, a concept that is similar to classical bits. We will see more explanations in later sections.

This quantum computer is accessible for free usage if you are living in Canada, America, Europe or Japan.

Last month, AWS announced a managed quantum computing service, Amazon Braket, that uses D-Wave 2000Q as its back-end.

The image above shows the quantum computer from Google, which they claimed to achieve quantum supremacy two months ago. It has 53 qubits effectively. It is open for research purposes, so it is not accessible for everyone.

The image above shows IBM Q. It has 53 qubits and is free for everyone. If you are interested in learning how to code and run it on real quantum computers, here is a hands-on tutorial that shows you how to do it.

What is quantum theory?

To understand quantum computing, and to explain why quantum computers are so large as we have seen in the above images, we must first talk about quantum theory. There is a few physics principles that explain how things work in different scales.

At the middle of the scale, that is the everyday scale we see, such as a car, a building, or a basketball, that’s governed by classical mechanics. Newton’s Laws work really well in this scale.

At a very large scale, something like a planet, Newton’s Laws do not apply. We need Einstein’s Relativity theory to explain things at this scale.

At a very, very tiny scale, at the size of an atom, people observed something that is really weird and cannot be explained by classical mechanics nor Relativity theory. So scientists have came up with quantum mechanics, which explains some tiny effects that could only be observed at this scale.

Double-slit experiment

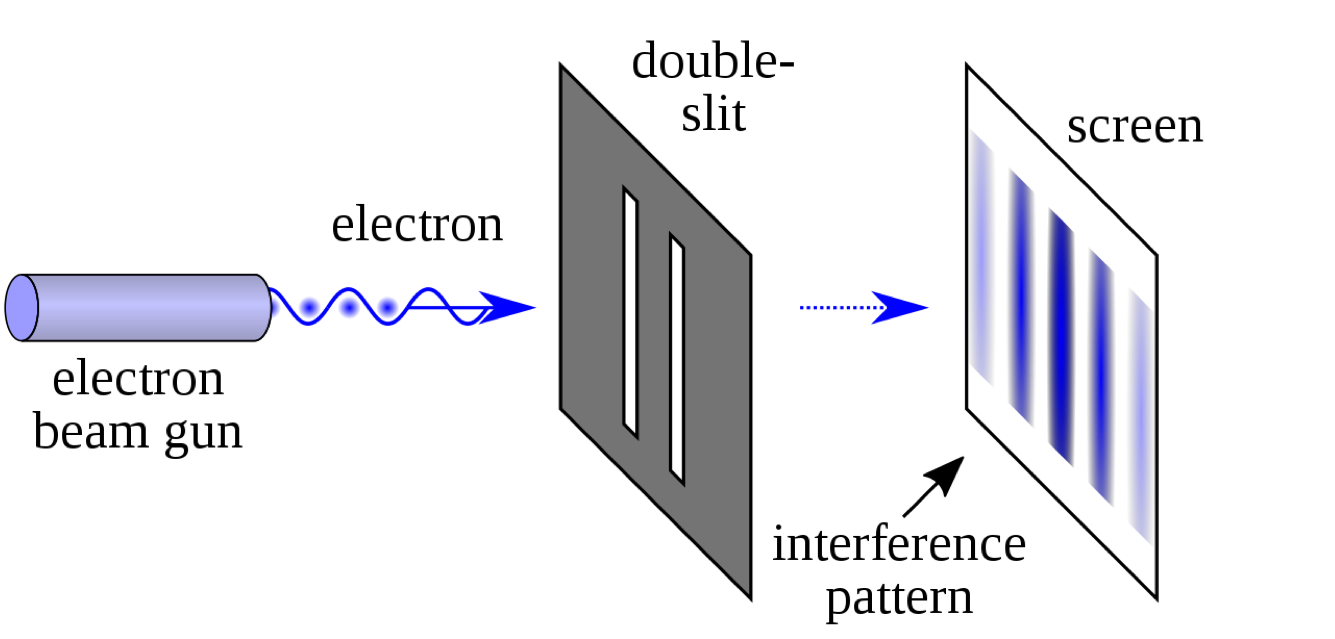
This is a double-slit experiment at a very small scale. On the left hand side, we have an electron gun, which fires electrons to the right. At the middle, we have a metal plate with two slits on it. The slits are very close to each other, such that an electron fired from the electron gun can randomly pass through either of the slits.

On the right hand side, we place a detector screen to absorb the energy of electrons that pass through the slits and hit the detector screen.

The band pattern on the detector screen is what we observed in this experiment. If you have studied physics in high school, you may recognize that we can get the same pattern by replacing electrons with water waves or light waves. It is the result of interference between two wave sources that pass through the slits.

This shows that electrons are particles and they have the properties of waves at the same time, so that when they pass through the slits, they generate this interference pattern.

One more remarkable thing about this experiment is, even if we fire just one electron, we can still get the same interference pattern. How can an electron interference with itself? Something in our understanding must be wrong.

Quantum theory suggests that the electron actually passes through both slits at the same time. The electron appears at two different locations at the same time such that the electron at different locations interferes with each other.

We cannot observe the moment the electron appears at both slits because the action to observe will corrupt this behavior. To observe, we must send some other signals, such as a light photon, to hit the electron, bounce back, and then we collect that photon and measure its energy. Such action will disturb the electron at this tiny scale. So there is absolutely no way to observe without destroying the experiment.

However, we can prove it by using mathematics. Consider if we have only one slit, and an electron passes through this slit and hits the detector screen at a certain point with a probability of p₁. Similarly, we have another slit with a probability of p₂ that an electron will pass through.

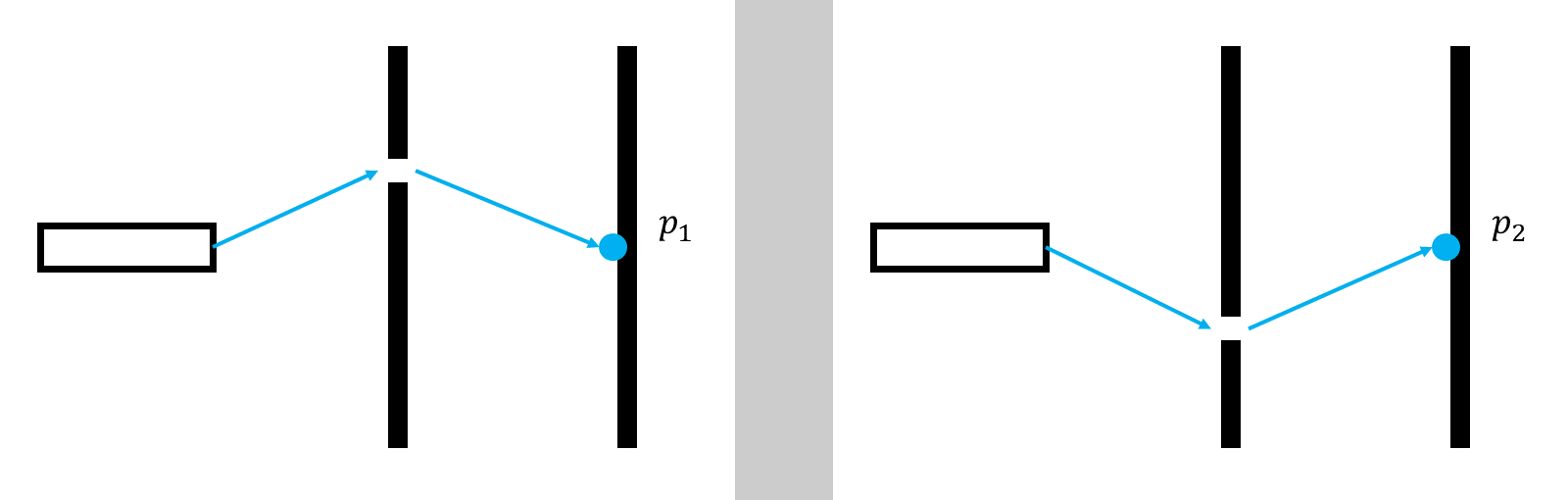
So what is the probability of an electron going through either slit? Because the slits are independent, this is a mutually exclusive event. The total probability should be p₁ + p₂, right?

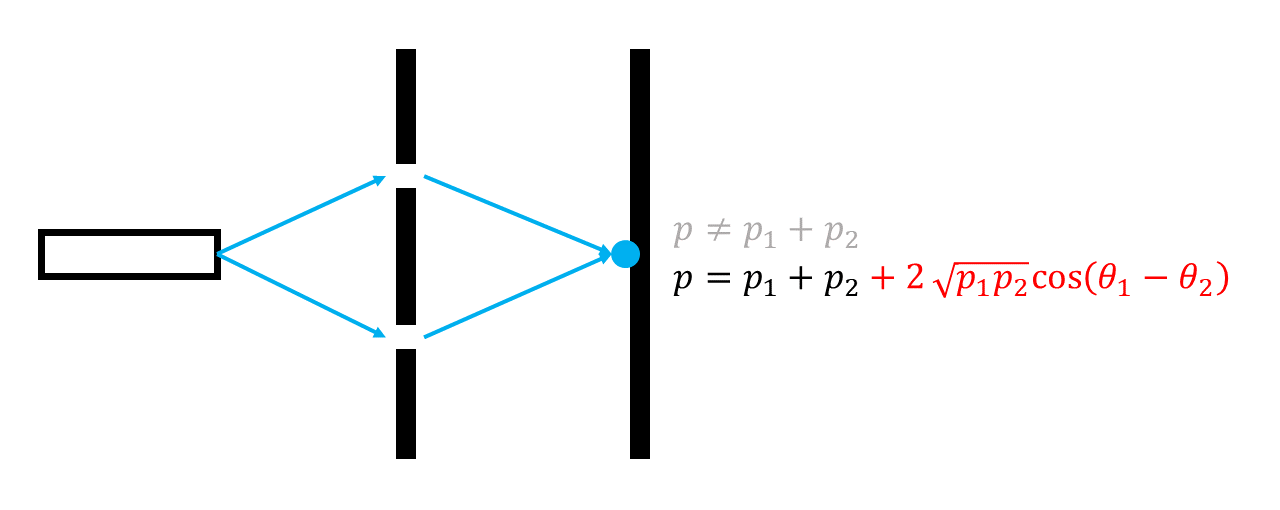
Wrong!

With some measurements, we know that it is p₁ plus p₂ plus something. This proves that this is not a mutually exclusive event. One explanation is that the electron has passed through both slits.

Superposition, randomness, and non-clonability

We used electrons in the above double-slit experiment. In fact, we could use other types of particle and we will get the same result. Any particles at this scale have the same quantum properties.

A particle is not static. It spins when it travels in space. It can spin upward or downward. More precisely, it spins upward and downward at the same time. This is called superposition. Once we observe it, the particle will have 50% of chance spinning upward, and 50% of chance spinning downward. With some measurements, we know that the direction of spinning is completely random.

As it spins in both directions at the same time, and when we observe it, it will randomly choose to spin in one direction, we cannot copy the spinning direction of one particle to another. This is the non-clonability property, which is the key element to create quantum encryption. If someone steals the encryption key, the information will be destroyed and thus no one can break quantum encryption.

Entanglement

If we put two particles close enough, they will somehow affect each other and correlate their spinning directions. This is call entanglement. When not observed, they keep in a superposition state. But once we observe either particle, if one particle, for example, spins upward, we know that the other particle must spin either upward or downward, depending on how they are entangled. That means once the first particle is observed, and its spinning direction will be chosen randomly, but the spinning direction of the second particle will no longer be chosen randomly. They are correlated.

How does a quantum computer work?

A classical computer processes bits of information as input, does some calculations and outputs the result. A quantum computer essentially works in the same way as a classical computer with the ability to process much more information in parallel. A quantum computer accepts qubits as its input, does some calculations using a tailor made quantum circuit and its output is observed.

Remember that the quantum properties are the key element for quantum computers to work. Quantum properties only work in a tiny scale and at this scale, these properties are easily destroyed because of interference and noises around the environment. In theory, a quantum computer could work perfectly if the environment is noise free, which happens only at absolute zero temperature (0 kelvin). What we can do is to create such an environment at a temperature slightly above absolute zero temperature by building huge infrastructures to cool the whole thing down. Unfortunately, noises are introduced as a result.

Therefore, at the last step where to get the output from a quantum computer, we perform the same calculation for a few more times, typically 1,000 times, for error correction due caused by environment noise.

Qubits

A qubit refers to a particle that has the quantum properties. It is like a classical bit. Both a qubit and a classical bit carry some information. A classical bit can either be 0 or 1, while a qubit is 0 and 1 at the same time if we consider 0 as spinning upward and 1 means spinning downward. That means one qubit carries two classical bits of information. So, with two qubits, we have 4 states in superposition. With N qubits, we have 2ᴺ states at the same time. That explains why a quantum computer is exponentially faster than a classical computer.

Quantum circuits

A quantum circuit is like an electronic circuit with some logic gates. We can manipulate the information that passes through the circuit. A quantum computer is the infrastructure that let pre-initialized qubits pass through a quantum circuit and observes the output.

Hands-on quantum programming

For software development folks, things get a little more interesting if you can get your hands dirty by programming on a real quantum computer. I have created a workshop-style tutorial to give you a head start. Do check it out!

Quantum computing 101: Workshop

08 Jan 2020 by Alan Tai

Comments powered by Disqus